Číselné systémy a podmínky

Tři hlavní oblasti rozdílu od našich čísel

Představte si, jak mnohem snazší by bylo naučit se aritmetice v prvních letech, kdyby se vše, co musíte udělat, bylo naučit psát řádek jako já a trojúhelník. To v podstatě museli dělat starověcí lidé z Mezopotámie, ačkoli je občas obměňovali, protahovali, otáčeli se atd.

Neměli na to naše tužky a tužky ani papír. Psali s pomocí nástroje, který by použil ve sochařství, protože médium bylo hlínou. Ať už je to těžší nebo snadnější se naučit manipulovat než tužkou, je to hodit nahoru, ale zatím jsou v oddělení snadnosti s pouhými dvěma základními symboly.

Další krok hodí klíč do oddělení jednoduchosti. Používáme a

V "Pocta Babylonii" [The Mathematical Gazette, Sv. 76, č. 475, „Využití dějin matematiky ve výuce matematiky“ (březen, 1992), s. 1, s. 158-178], spisovatel-učitel Nick Mackinnon říká, že používá babylonskou matematiku k výuce 13letých dětí o základnách jiných než 10. Babylonský systém používá základnu 60, což znamená, že místo desetinného čísla je to sexagesimální.

Babylonský systém čísel i náš spoléhají na to, že dávají hodnotu. Oba systémy to dělají jinak, částečně proto, že jejich systém postrádal nulu. Učení babylonského polohového systému zleva doprava (od nejvyšší k nejnižší) pro první vkus základní aritmetiky už pravděpodobně neexistuje obtížné než naučit se naše dvousměrné, kde si musíme pamatovat pořadí desetinných čísel - zvyšující se od desetinných, ty, desítky, stovky, a pak se vyfouknou opačným směrem na druhé straně, žádný sloupec, jen desetiny, setiny, tisíciny atd.

Na dalších stránkách se budu věnovat pozicím babylonského systému, nejdřív se však musím naučit několik důležitých čísel.

Mluvíme o obdobích let pomocí desetinných množství. Máme deset let na deset let, století na 100 let (10 dekád) nebo 10X10 = 10 let na druhou a tisíciletí na 1000 let (10 století) nebo 10X100 = 10 let krychlových. Nevím o žádném vyšším termínu, ale to nejsou jednotky, které Babyloňané používali. Nick Mackinnon odkazuje na tabletu od Senkareha (Larsa) od sira Henryho Rawlinsona (1810 - 1895) * pro jednotky, které používali Babyloňané, a to nejen pro příslušné roky, ale také pro předpokládaná množství:

1. soss
2. ner
3. sar.

sossnersosssarsoss

Stále žádný remorkér: Není nutně snazší naučit se odvozené podmínky na druhou a krychlový rok z latiny, než je to slabika babylonských, která nezahrnují krychlování, ale násobení 10.

Co myslíš? Bylo by těžší naučit se základům čísel jako babylonského školního dítěte nebo jako moderního studenta anglicky mluvící školy?

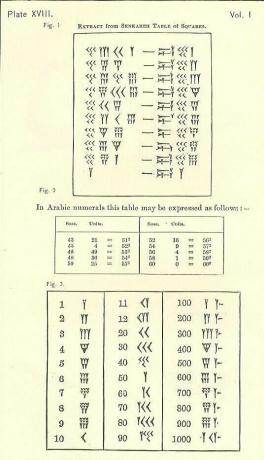
George Rawlinson (1812-1902), Henryův bratr, ukazuje zjednodušenou přepsanou tabulku čtverců v Sedm velkých monarchií starověkého východního světa. Tabulka se zdá být astronomická, založená na kategoriích babylonských let.

Všechny fotografie pocházejí z této online naskenované verze vydání George Rawlinsona z 19. století Sedm velkých monarchií starověkého východního světa.

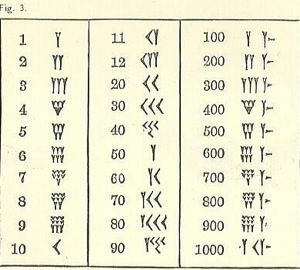
Protože jsme vyrůstali s jiným systémem, babylonská čísla jsou matoucí.

Alespoň čísla běží zleva doleva doprava, stejně jako náš arabský systém, ale zbytek se pravděpodobně bude zdát neznámý. Symbolem pro jeden je klínový nebo Y tvar. Bohužel Y také představuje 50. Existuje několik samostatných symbolů (všechny založené na klínu a čáře), ale všechna ostatní čísla jsou z nich vytvořena.

Pamatujte, že forma psaní je klínový tvar nebo klínovitého tvaru. Z důvodu nástroje, který se používá k kreslení čar, existuje omezená rozmanitost. Klín může nebo nemusí mít ocas, natažený tahem stylusu pro psaní klínového tvaru podél hlíny po otisku tvaru trojúhelníku.

10, které jsou popisovány jako hrot šípu, vypadá jako trochu jako natažené.

Tři řady až 3 malých 1s (psaných jako Ys s některými zkrácenými ocasy) nebo 10s (10 je psáno jako

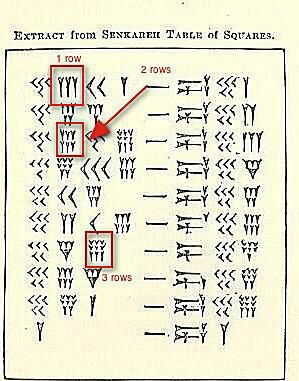
Existují tři sady klínového čísla shluky zvýrazněno na obrázku výše.

Teď se nezajímáme o jejich hodnotu, ale o to, jak byste mohli vidět (nebo psát) kdekoli od 4 do 9 stejného čísla seskupeného dohromady. Tři jdou v řadě. Pokud existuje čtvrtá, pátá nebo šestá, jde dolů. Pokud existuje sedmý, osmý nebo devátý, potřebujete třetí řádek.

Následující stránky pokračují s pokyny pro provádění výpočtů s babylonskou klínovou tváří.

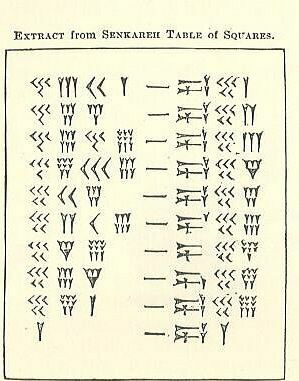
Z toho, co jste četli výše o soss - na které si vzpomínáte, že je Babylonian po dobu 60 let, klín a hrot šípu - což jsou popisná jména pro klínové značky, zjistěte, zda můžete zjistit, jak tyto výpočty fungují. Jedna strana čárkované značky je číslo a druhá je čtverec. Zkuste to jako skupina. Pokud na to nemůžete přijít, podívejte se na další krok.

Dokážete to přijít hned teď? Dejte mu šanci.

...

Na levé straně jsou 4 jasné sloupce následované pomlčkou a 3 sloupce na pravé straně. Při pohledu na levou stranu je ekvivalentem sloupce 1s ve skutečnosti 2 sloupce nejblíže k „pomlčce“ (vnitřní sloupce). Další 2 vnější sloupce se počítají společně jako sloupec 60. let.

• 4-
• 3-Ys = 3.
• 40+3=43.
• Jediným problémem je, že za nimi je další číslo. To znamená, že to nejsou jednotky (místo těch '). 43 není 43-ti, ale 43-60s, protože je to sexagesimální (základní-60) systém a je v soss sloupec, jak ukazuje spodní tabulka.
• Vynásobte 43 x 60 a získáte 2580.
• Přidat další číslo (2-
• Nyní máte 2601.
• To je náměstí 51.

Další řádek má 45 v soss sloupec, takže vynásobte 45 x 60 (nebo 2700) a poté přidejte 4 ze sloupce jednotek, takže máte 2704. Druhá odmocnina 2704 je 52.

Dokážete zjistit, proč je poslední číslo = 3600 (60 na druhou)? Tip: Proč to není 3000?